Publications
2023
-
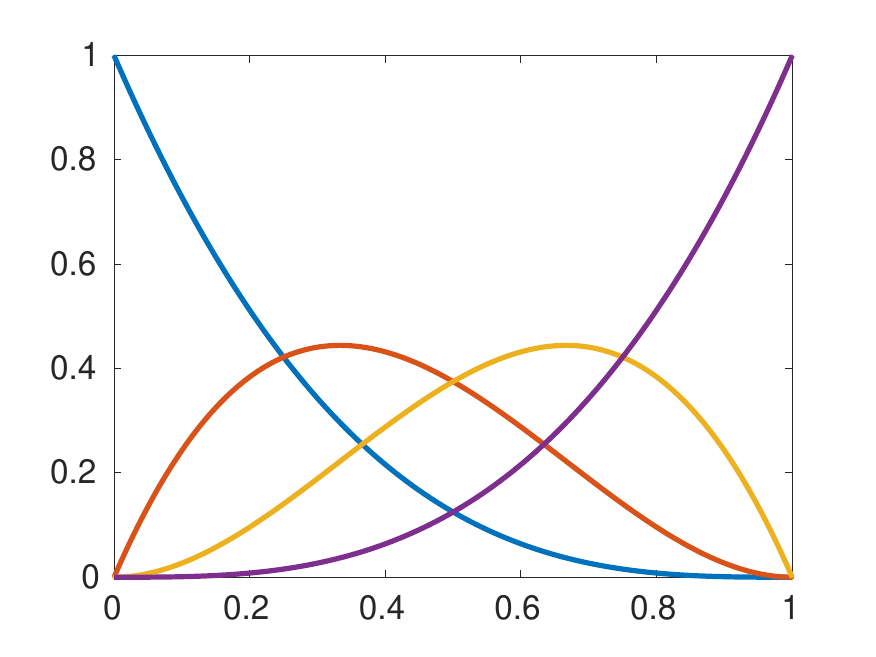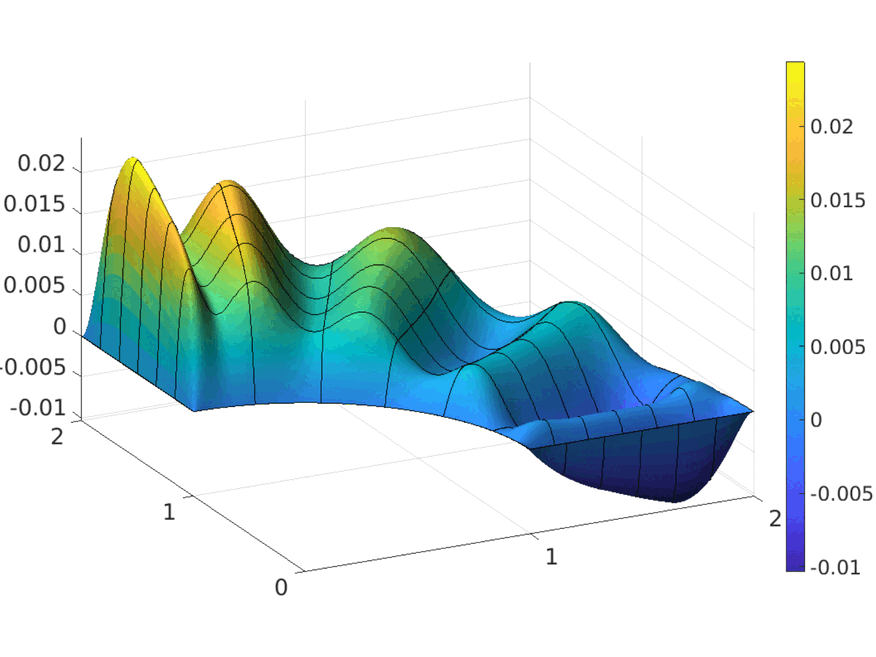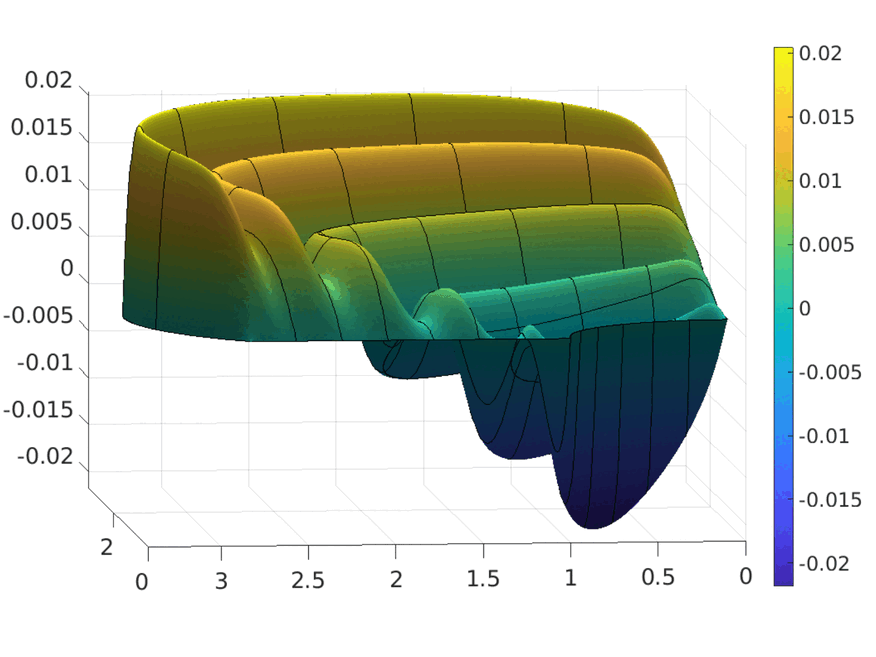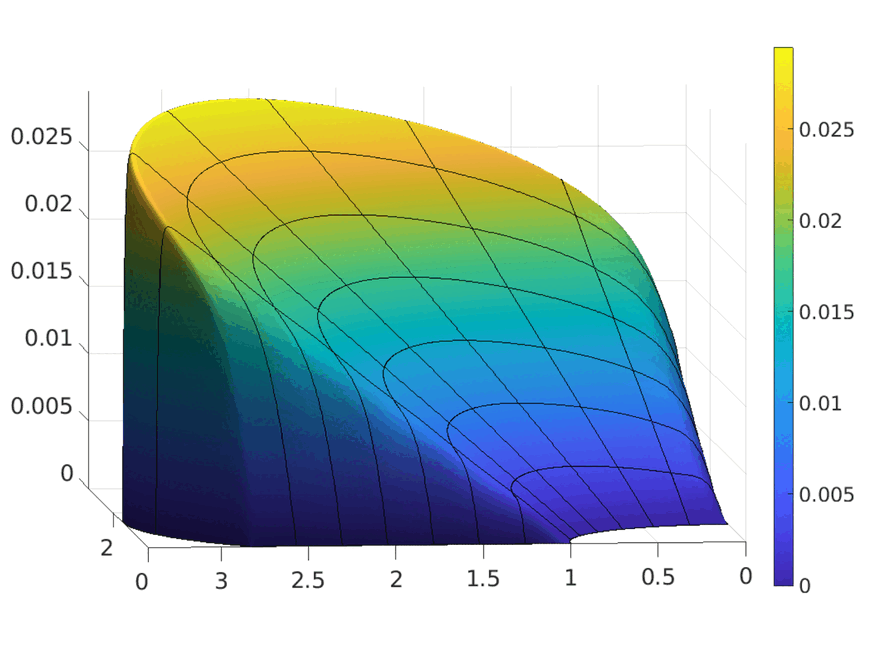 Tchebycheffian B-splines in isogeometric Galerkin methodsKrunal Raval, Carla Manni, and Hendrik SpeleersComputer Methods in Applied Mechanics and Engineering, 2023
Tchebycheffian B-splines in isogeometric Galerkin methodsKrunal Raval, Carla Manni, and Hendrik SpeleersComputer Methods in Applied Mechanics and Engineering, 2023Tchebycheffian splines are smooth piecewise functions whose pieces are drawn from (possibly different) Tchebycheff spaces, a natural generalization of algebraic polynomial spaces. They enjoy most of the properties known in the polynomial spline case. In particular, under suitable assumptions, Tchebycheffian splines admit a representation in terms of basis functions, called Tchebycheffian B-splines (TB-splines), completely analogous to polynomial B-splines. A particularly interesting subclass consists of Tchebycheffian splines with pieces belonging to null-spaces of constant-coefficient linear differential operators. They grant the freedom of combining polynomials with exponential and trigonometric functions with any number of individual shape parameters. Moreover, they have been recently equipped with efficient evaluation and manipulation procedures. In this paper we consider the use of TB-splines with pieces belonging to null-spaces of constant-coefficient linear differential operators as an attractive substitute for standard polynomial B-splines and rational NURBS in isogeometric Galerkin methods. We discuss how to exploit the large flexibility of the geometrical and analytical features of the underlying Tchebycheff spaces according to problem-driven selection strategies. TB-splines offer a wide and robust environment for the isogeometric paradigm beyond the limits of the rational NURBS model.
@article{raval2023tchebycheffian, title = {Tchebycheffian {B}-splines in isogeometric {Galerkin} methods}, author = {Raval, Krunal and Manni, Carla and Speleers, Hendrik}, journal = {Computer Methods in Applied Mechanics and Engineering}, volume = {403}, pages = {115648}, year = {2023}, publisher = {Elsevier}, doi = {10.1016/j.cma.2022.115648}, }
2024
-
 Adaptive isogeometric analysis based on Locally Refined Tchebycheffian B-splinesKrunal Raval, Carla Manni, and Hendrik SpeleersComputer Methods in Applied Mechanics and Engineering, 2024
Adaptive isogeometric analysis based on Locally Refined Tchebycheffian B-splinesKrunal Raval, Carla Manni, and Hendrik SpeleersComputer Methods in Applied Mechanics and Engineering, 2024We introduce locally refined (LR) Tchebycheffian B-splines as a generalization of LR B-splines from the algebraic polynomial setting to the broad Tchebycheffian setting. We focus on the particularly interesting class of Tchebycheffian splines whose pieces belong to null-spaces of constant-coefficient linear differential operators. They offer the freedom of combining algebraic polynomials with exponential and trigonometric functions with any number of individual shape parameters and have been recently equipped with efficient evaluation and manipulation procedures. We consider their application in the context of isogeometric analysis and discuss related adaptive refinement, adopting the so-called structured mesh refinement strategy, widely used and analyzed in the classical polynomial case.
@article{raval2024tchebycheffianLR, title = {{A}daptive isogeometric analysis based on {L}ocally {R}efined {T}chebycheffian {B}-splines}, author = {Raval, Krunal and Manni, Carla and Speleers, Hendrik}, journal = {Computer Methods in Applied Mechanics and Engineering}, volume = {430}, pages = {117186}, year = {2024}, publisher = {Elsevier}, doi = {10.1016/j.cma.2024.117186}, } - Local h-, p- and k-adaptivity with LR B-splinesKrunal Raval, René R. Hiemstra, Kjetil André Johannessen, and 1 more authorin preparation, 2024
Locally Refined B-splines (LR B-splines) have proven a very flexible and powerful framework in several applications, such as, interpolation and data reconstruction, Computer Aided Design (CAD) and IsoGeometric Analysis (IGA). In this work we extend LR B-splines to allow for non-uniform polynomial degree. This capability, combined with local \emphh-refinement, also allows for local \emphk-refinement, that is, increasing the polynomial degree as well as the smoothness at newly introduced knot lines. The novel refinement schemes are based on degree elevation of individual basis functions by means of certain two-scale relations, and lead to nested spaces. We study the properties of the introduced spaces and apply them to several two-dimensional model problems, illustrating the efficacy of the proposed adaptive refinement methodology in the context of IsoGeometric Analysis.
- Non-uniform degree and Tchebycheffian spline technologies for adaptive isogeometric analysisKrunal Raval2024
Tchebycheffian splines are smooth piecewise functions whose pieces are drawn from (possibly different) Tchebycheff spaces, a natural generalization of algebraic polynomial spaces. They enjoy most of the properties known in the polynomial spline case. In particular, under suitable assumptions, Tchebycheffian splines admit a representation in terms of basis functions, called Tchebycheffian B-splines (TB-splines), completely analogous to polynomial B-splines. A particularly interesting subclass consists of Tchebycheffian splines with pieces belonging to null-spaces of constant-coefficient linear differential operators. They grant the freedom of combining polynomials with exponential and trigonometric functions with any number of individual shape parameters. Moreover, they have been recently equipped with efficient evaluation and manipulation procedures. We consider the use of TB-splines with pieces belonging to null-spaces of constant-coefficient linear differential operators as an attractive substitute for standard polynomial B-splines and rational NURBS in isogeometric Galerkin methods. We discuss how to exploit the large flexibility of the geometrical and analytical features of the underlying Tchebycheff spaces according to problem-driven selection strategies. TB-splines offer a wide and robust environment for the isogeometric paradigm beyond the limits of the rational NURBS model. Locally Refined B-splines (LR B-splines) have proven to be a very flexible and powerful framework in several application areas, such as approximation and data reconstruction, computer aided design, and isogeometric analysis. We introduce Locally Refined Tchebycheffian B-splines (LR TB-splines) as a generalization of LR B-splines from the algebraic polynomial setting to the broad Tchebycheffian setting. We focus again on the particularly interesting class of Tchebycheffian splines whose pieces belong to null-spaces of constant-coefficient linear differential operators. We consider their application in the context of isogeometric analysis and discuss related adaptive refinement, adopting the so-called structured mesh refinement strategy, widely used and analyzed in the classical polynomial case. Finally, we extend LR B-splines to allow for non-uniform polynomial degree. This capability, combined with local h-refinement, also allows for local hp-refinement, that is, increasing the polynomial degree as well as the smoothness at newly introduced knot lines. The novel refinement schemes are based on degree elevation of individual basis functions by means of certain two-scale relations, and lead to nested spaces. We apply the introduced spaces to several two-dimensional model problems, illustrating the efficacy of the proposed adaptive refinement methodology in the context of isogeometric analysis.